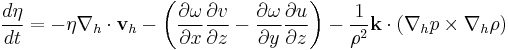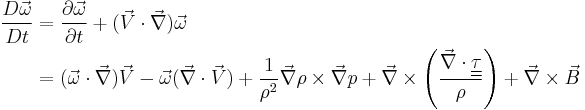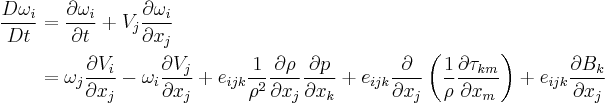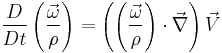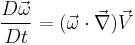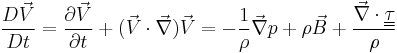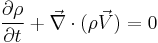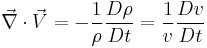Vorticity equation

The vorticity equation is an important prognostic equation in the atmospheric sciences. Vorticity is a vector, therefore, there are three components. The equation of vorticity (three components in the canonical form) describes the material derivative (that is, the local change due to local change with time and advection) of vorticity, and thus can be stated in either relative or absolute form.

The more compact version is that for absolute vorticity, component 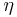$\eta$ , using the pressure system:

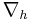$\frac{d \eta}{d t} = -\eta \nabla_h \cdot\mathbf{v}_h - \left( \frac{\partial \omega}{\partial x} \frac{\partial v}{\partial z} - \frac{\partial \omega}{\partial y} \frac{\partial u}{\partial z} \right) - \frac{1}{\rho^2} \mathbf{k} \cdot ( \nabla_h p \times \nabla_h \rho )$

Here, $\rho$ is density, u, v, and $\omega$ are the components of wind velocity, and $\nabla_h$ is the 2-dimensional (i.e. horizontal-component-only) del.

The terms on the RHS denote the positive or negative generation of absolute vorticity by divergence of air, twisting of the axis of rotation, and baroclinity, respectively.

1 Fluid dynamics
- 1.1 Physical Interpretation
- 1.2 Simplifications
2 Notes
3 References
4 See also

Fluid dynamics

The vorticity equation describes the evolution of the vorticity 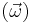$(\vec \omega)$ of a fluid element as it moves around. The vorticity equation can be derived from the conservation of momentum equation.^[1] In its general vector form it may be expressed as follows,

$\begin{align} \frac{D\vec\omega}{Dt} &= \frac{\partial \vec \omega}{\partial t} %2B (\vec V \cdot \vec \nabla) \vec \omega \\ &= (\vec \omega \cdot \vec \nabla) \vec V - \vec \omega (\vec \nabla \cdot \vec V) %2B \frac{1}{\rho^2}\vec \nabla \rho \times \vec \nabla p %2B \vec \nabla \times \left( \frac{\vec \nabla \cdot \underline{\underline{\tau}}}{\rho} \right) %2B \vec \nabla \times \vec B \end{align}$

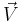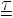where, $\vec V$ is the velocity vector, $\rho$ is the density, $p$ is the pressure, $\underline{\underline{\tau}}$ is the viscous stress tensor and 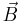$\vec B$ is the body force term.

Equivalently in tensor notation,

$\begin{align} \frac{D\omega_i}{Dt} &= \frac{\partial \omega_i}{\partial t} %2B V_j \frac{\partial \omega_i}{\partial x_j} \\ &= \omega_j \frac{\partial V_i}{\partial x_j} - \omega_i \frac{\partial V_j}{\partial x_j} %2B e_{ijk}\frac{1}{\rho^2}\frac{\partial \rho}{\partial x_j}\frac{\partial p}{\partial x_k} %2B e_{ijk}\frac{\partial}{\partial x_j}\left(\frac{1}{\rho}\frac{\partial \tau_{km}}{\partial x_m}\right) %2B e_{ijk}\frac{\partial B_k }{\partial x_j} \end{align}$

where, we have used the Einstein summation convention, and 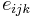$e_{ijk}$ is the Levi-Civita symbol.

Physical Interpretation

The term 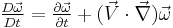$\tfrac{D\vec\omega}{Dt} = \tfrac{\partial \vec \omega}{\partial t} %2B (\vec V \cdot \vec \nabla) \vec \omega$ is the material derivative of the vorticity vector 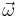$\vec \omega$ . It describes the rate of change of vorticity of a fluid particle (or in other words the angular acceleration of the fluid particle). This can change due to the unsteadiness in the flow captured by 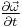$\tfrac{\partial \vec \omega}{\partial t}$ (the unsteady term) or due to the motion of the fluid particle as it moves from one point to another, 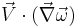$\vec V \cdot (\vec \nabla \vec \omega)$ (the convection term).

The first term on the RHS of the vorticity equation, 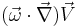$(\vec \omega \cdot \vec \nabla) \vec V$ , describes the stretching or tilting of vorticity due to the velocity gradients. Note that 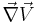$\vec \nabla \vec V$ is a tensor with nine terms.

The next term, 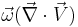$\vec \omega (\vec \nabla \cdot \vec V)$ , describes stretching of vorticity due to flow compressibility.^[2] Sometimes the negative sign is included in the term.

The third term, 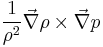$\frac{1}{\rho^2}\vec \nabla \rho \times \vec \nabla p$ is the baroclinic term. It accounts for the changes in the vorticity due to the intersection of density and pressure surfaces.

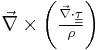$\vec \nabla \times \left( \tfrac{\vec \nabla \cdot \underline{\underline{\tau}}}{\rho} \right)$ , accounts for the diffusion of vorticity due to the viscous effects.

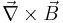$\vec \nabla \times \vec B$ provides for changes due to body forces.^[3]

Simplifications

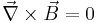In case of conservative body forces, $\vec \nabla \times \vec B = 0$ .
For a barotropic fluid, 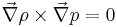$\vec \nabla \rho \times \vec \nabla p = 0$ . This is also true for a constant density fluid where 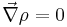$\vec \nabla \rho = 0$ .^[4]
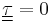For inviscid fluids, $\underline{\underline{\tau}} = 0$ .

Thus for an inviscid, barotropic fluid with conservative body forces, the vorticity equation simplifies to, ^[5]

$\frac{D}{Dt} \left( \frac{\vec \omega}{\rho} \right) = \left( \left( \frac{\vec\omega}{\rho} \right) \cdot \vec \nabla \right) \vec V$

Alternately, in case of incompressible, inviscid fluid with conservative body forces,

$\frac{D \vec \omega}{Dt} = (\vec \omega \cdot \vec \nabla) \vec V$

Notes

^ Derivation of the vorticity equation In the absence of any concentrated torques and line forces, the momentum conservation equation gives,

$\frac{D \vec V}{D t} = \frac{\partial \vec V}{\partial t} %2B (\vec V \cdot \vec \nabla) \vec V = - \frac{1}{\rho} \vec \nabla p %2B \rho \vec B %2B \frac{\vec \nabla \cdot \underline{\underline{\tau}}}{\rho}$

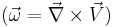Now, vorticity is defined as the curl of the velocity vector $( \vec \omega = \vec \nabla \times \vec V)$ . Taking curl of momentum equation yields the desired equation. The following identities are useful in derivation of the equation,

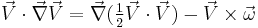
$\vec V \cdot \vec \nabla \vec V = \vec \nabla (\tfrac{1}{2} \vec V \cdot \vec V) - \vec V \times \vec \omega$

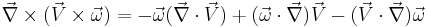
$\vec \nabla \times (\vec V \times \vec \omega ) = -\vec \omega (\vec \nabla \cdot \vec V) %2B (\vec \omega \cdot \vec \nabla ) \vec V - (\vec V \cdot \vec \nabla) \vec \omega$

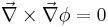$\vec \nabla \times \vec \nabla \phi = 0$ , where $\phi$ is a scalar.

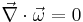
$\vec \nabla \cdot \vec \omega = 0$
^ The flow continuity equation states that,

$\frac{\partial \rho}{\partial t} %2B \vec \nabla \cdot(\rho \vec V) = 0$

This can be rewritten as,

$\vec \nabla \cdot \vec V = -\frac{1}{\rho} \frac{D \rho}{Dt} = \frac{1}{v} \frac{Dv}{Dt}$

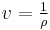where $v = \tfrac{1}{\rho}$ is the specific volume of the fluid element. Thus one can think of 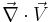$\vec \nabla \cdot \vec V$ as a measure of flow compressibility.
^ A body force is one which is proportional to mass/volume/charge on a body. Such forces act over the whole volume of the body as opposed to a surface forces which act only on the surface. Examples of body forces are gravitational force, electromagnetic force, etc. Examples of surface forces are friction, pressure force, etc. Also there are line forces, like surface tension.
^ Note that incompressible fluid (constant density fluid) is not same as incompressible flow and the barotropic term can not be neglected in case of incompressible flow.
^ We use the continuity equation to get to this form.

References

Utpal Manna and S. S. Sritharan (2007), "Lyapunov Functionals and Local Dissipativity for the Vorticity Equation in L^p and Besov spaces,", Differential and Integral Equations, 20 (5): 581–598.
V. Barbu and S. S. Sritharan, “M-accretive Quantization of the Vorticity Equation", in Semi-groups of Operators: Theory and Applications, edited by A. V. Balakrishnan, Birkhauser, Boston, 2000, pp. 296-303. http://www.nps.edu/Academics/Schools/GSEAS/SRI/BookCH12.pdf